Clustering masuk dalam kategori unsupervised learning karena model ini dipakai pada data yang tidak memiliki label. Menurut Andriy Burkov dalam buku The Hundred Page Machine Learning Book, clustering atau pengklasteran adalah sebuah metode untuk memberi label pada data tanpa bantuan manusia. Bagaimana proses pemberian label ini?
Data yang memiliki kemiripan akan dikelompokkan lalu, setiap data pada kelompok yang sama akan diberikan label yang sama.
Berbeda kan, dengan model klasifikasi dan regresi di mana setiap data memiliki label yang ditulis oleh manusia.
Pada submodul ini kita akan belajar mengenai salah satu metode clustering yang sangat populer yaitu K-Means clustering.
K-Means Clustering
Pengklasteran K-Means adalah sebuah metode yang dikembangkan oleh Stuart Lloyd dari Bell Labs pada tahun 1957. Lloyd menggunakan metode ini untuk mengubah sinyal analog menjadi sinyal digital. Proses pengubahan sinyal ini juga dikenal sebagai Pulse Code Modulation.
Pada awalnya metode K-means hanya dipakai untuk internal perusahaan. Metode ini baru dipublikasikan sebagai jurnal ilmiah pada tahun 1982. Pada tahun 1965, Edward W. Forgy mempublikasikan metode yang sama dengan K-Means, sehingga K-Means juga dikenal sebagai metode Lloyd-Forgy.
Untuk melihat bagaimana K-Means bekerja, kita akan menggunakan data seperti di bawah ini. Perhatikan bahwa data yang kita gunakan terdapat 12 sampel dan data ini merupakan data 1 dimensi.
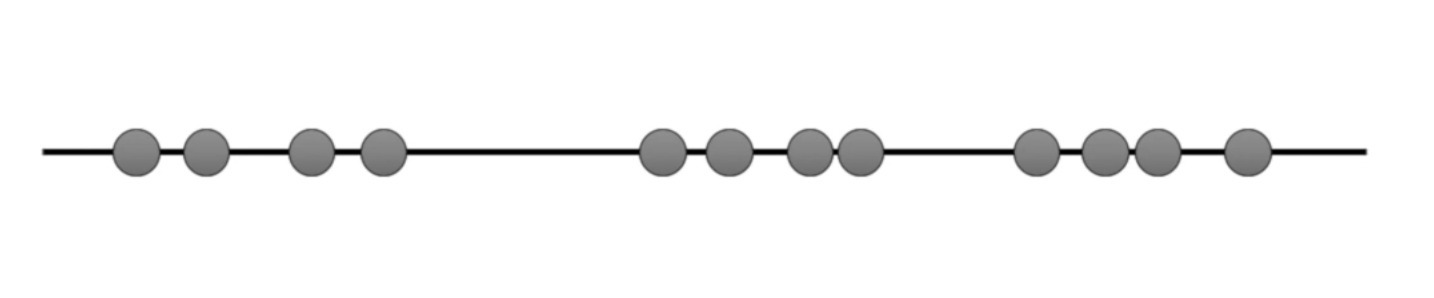

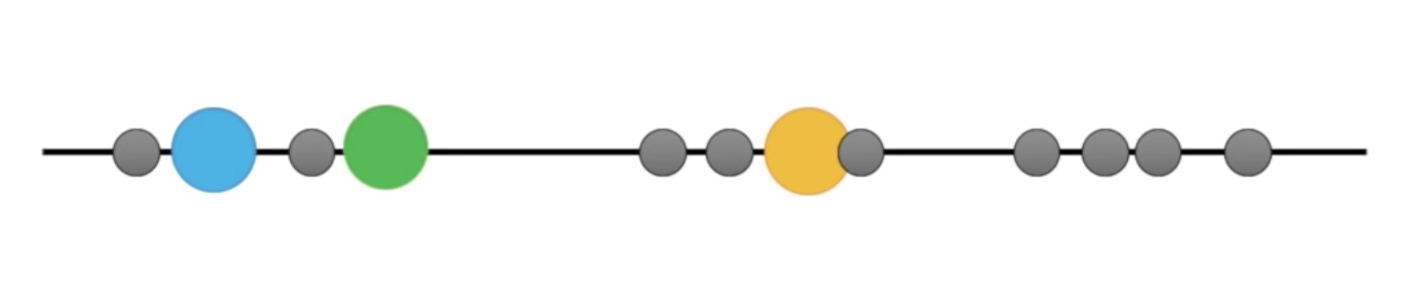
Hal yang paling pertama K-Means lakukan adalah memilih sebuah sampel secara acak untuk dijadikan centroid. Centroid adalah sebuah sampel pada data yang menjadi pusat dari sebuah cluster. Kita bisa melihat pada gambar bahwa 3 sampel yang dijadikan centroid diberi warna biru, hijau dan kuning.

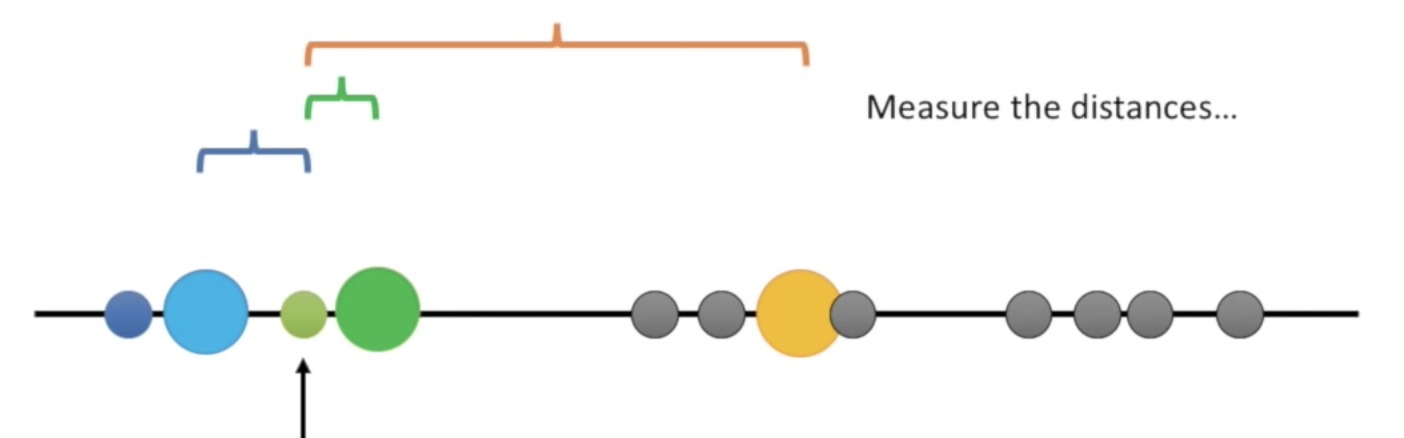
Kedua, karena centroid adalah pusat dari sebuah cluster, setiap sampel akan masuk ke dalam cluster. Ini bermula dari centroid terdekat dengan sampel tersebut. Pada contoh di bawah sampel yang ditunjuk anak panah memiliki jarak terdekat dengan centroid warna hijau. Alhasil, sampel tersebut masuk ke dalam cluster hijau.

Berikut adalah hasil ketika tahap kedua selesai.


Ketiga, setelah setiap sampel dimasukkan pada cluster dari centroid terdekat, K-Means akan menghitung rata-rata dari setiap sampel dan menjadikan rata-rata tersebut sebagai centroid baru. Rata-rata di sini adalah titik tengah dari setiap sampel pada sebuah cluster. Pada gambar dibawah rata-rata yang menjadi centroid baru digambarkan sebagai garis tegak lurus.


Keempat, langkah kedua diulang kembali. Sampel akan dimasukkan ke dalam cluster dari centroid baru yang paling dekat dengan sampel tersebut.


Pada tahap ini Anda mengulangi langkah ketiga, yaitu menemukan rata-rata dari cluster terbaru. Anda akan menemukan rata-rata tiap cluster di tahap keempat akan sama dengan rata-rata tiap cluster pada tahap ketiga sehingga centroidnya tidak berubah. Ketika centroid baru tidak ditemukan, maka proses clustering berhenti.
Apakah prosesnya telah selesai?. Seperti yang bisa kita lihat, hasil pengklasteran dari tahapan sebelumnya belum terlihat optimal.
Untuk mengukur kualitas dari pengklasteran, K-Means akan melakukan iterasi lagi dan mengulangi lagi tahap pertama yaitu memilih sampel secara acak untuk dijadikan centroid. Gambar di bawah menunjukkan K-Means pada iterasi kedua mengulangi kembali langkah pertama yaitu memilih centroid secara acak.


Untuk iterasi kedua, Anda bisa mempraktekkan langkah yang sudah dijelaskan sebelumnya untuk menguji pemahaman Anda.Hasil dari iterasi kedua adalah sebagai berikut.


Hasil dari iterasi kedua terlihat lebih baik dibanding iterasi pertama. Untuk membandingkan cluster setiap iterasi, K-Means akan menghitung variance dari tiap iterasi. Variance adalah persentase jumlah sampel pada tiap cluster. Gambar di bawah menunjukkan variance pada iterasi pertama.
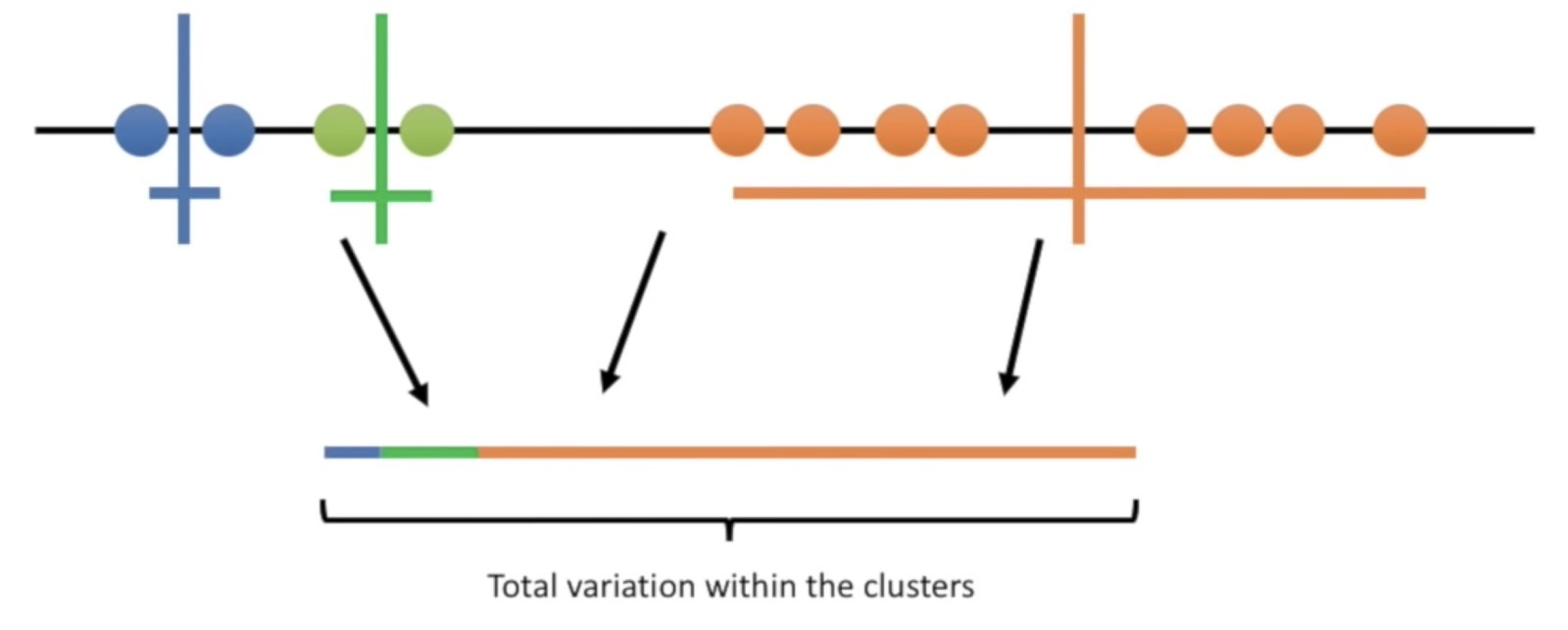

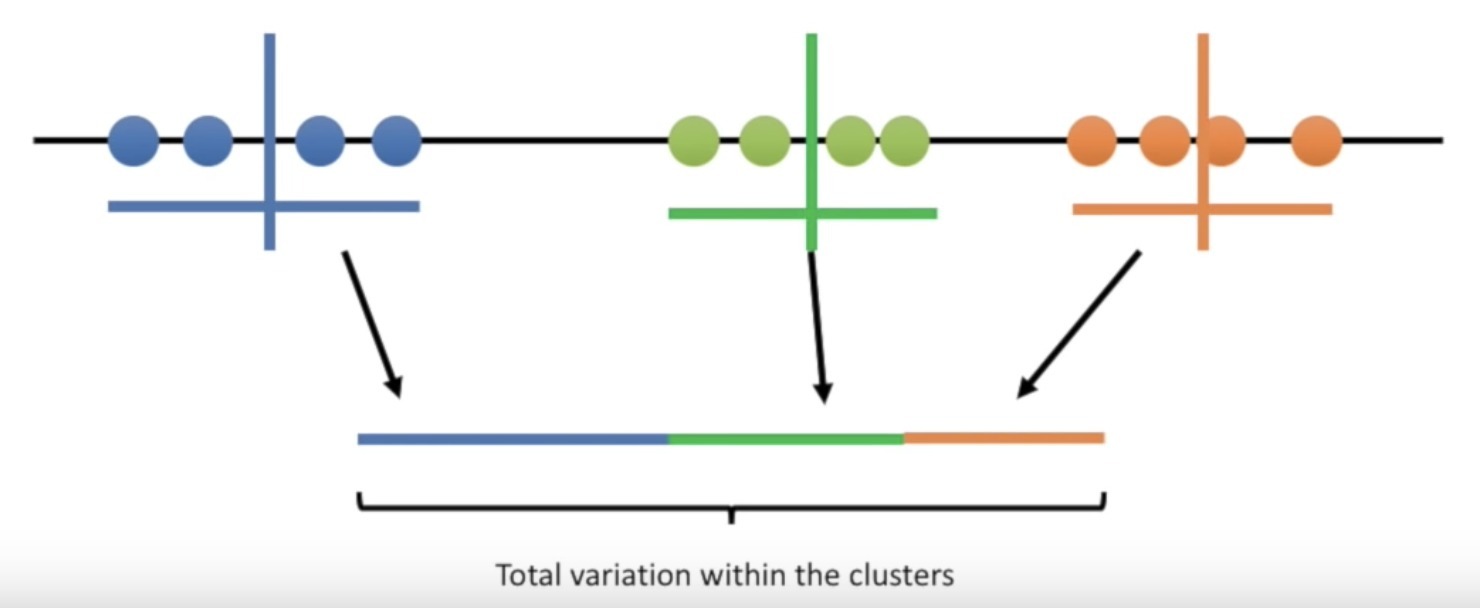
Kita bisa melihat bahwa di iterasi kedua, variance nya lebih seimbang dan tidak condong pada cluster tertentu. Sehingga, hasil dari cluster iterasi kedua lebih baik dari iterasi pertama. Jumlah iterasi dari K-Means ditentukan oleh programmer, dan K-Means akan berhenti melakukan iterasi sampai batas yang telah ditentukan.
Untuk data yang memiliki 2 dimensi atau lebih, k-means bekerja dengan sama yaitu menentukan centroid secara acak, lalu memindahkan centroid sampai posisi centroid tidak berubah. Animasi di bawah akan membantu Anda untuk melihat bagaimana K-Means bekerja pada data 2 dimensi.


Metode Elbow
Cara paling mudah untuk menentukan jumlah K atau cluster pada K-means adalah dengan melihat langsung persebaran data. Otak kita bisa mengelompokkan data-data yang berdekatan dengan sangat cepat. Tetapi cara ini hanya bekerja dengan baik pada data yang sangat sederhana.
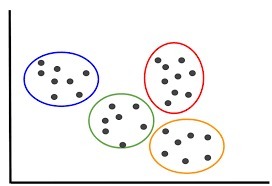
Ketika masalah clustering lebih kompleks seperti gambar dibawah, dan kita bingung menentukan jumlah cluster yang pas, kita bisa menggunakan metode Elbow.


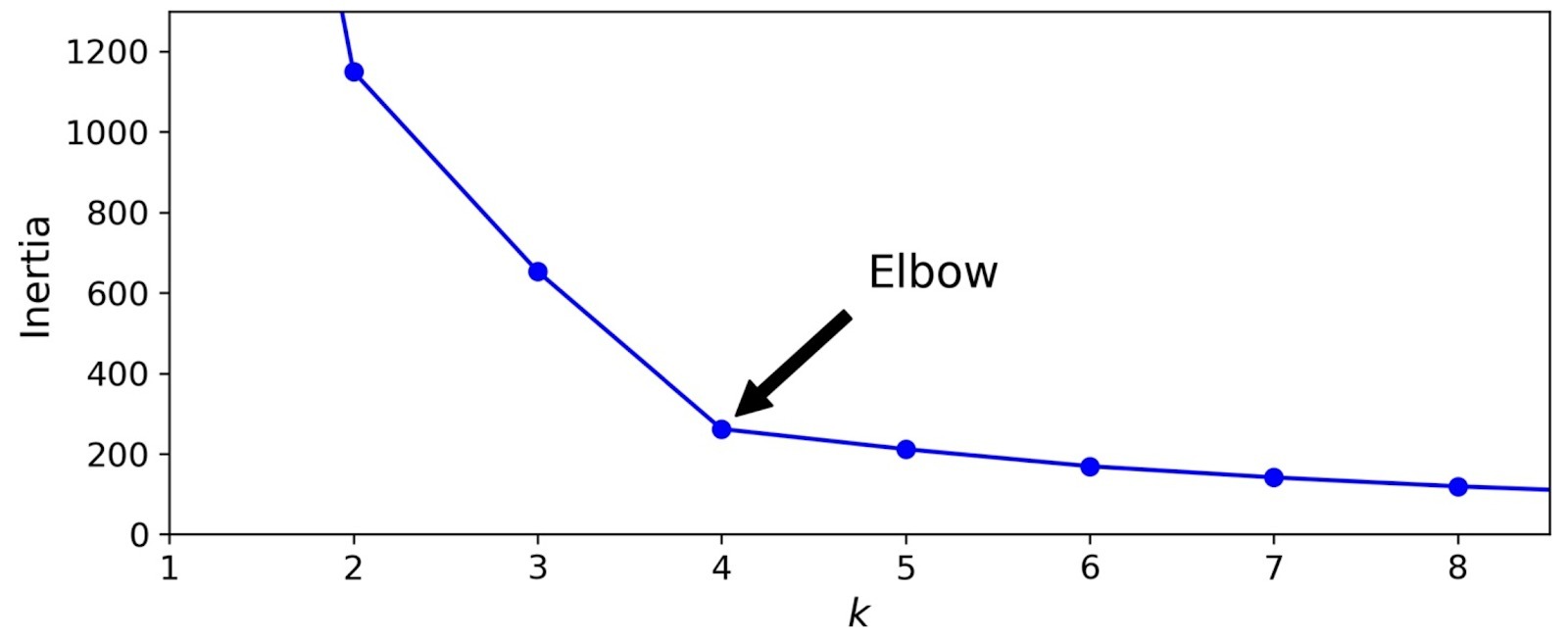
Ide mendasar dari metode elbow adalah untuk menjalankan K-Means pada dataset dengan nilai K pada jarak tertentu (1,2,3, .., N). Kemudian hitung inersia pada setiap nilai K. Inersia memberi tahu seberapa jauh jarak setiap sampel pada sebuah cluster. Semakin kecil inersia maka semakin baik karena jarak setiap sampel pada sebuah klaster lebih berdekatan.
Metode elbow bertujuan untuk menentukan elbow, yaitu jumlah K yang optimal. Untuk menentukan elbow, kita perlu melakukannya secara manual, yaitu dengan melihat titik dimana penurunan inersia tidak lagi signifikan.
Pada contoh di bawah kita memiliki data yang dapat dibagi menjadi 4 klaster. Bagaimana metode elbow dapat menentukan jumlah klaster tersebut optimal?

Kita akan mengaplikasikan metode elbow pada data di atas. Elbow berada di nilai K sama dengan 4, karena penurunan inersia pada K seterusnya tidak lagi signifikan (perubahannya nilainya kecil). Sehingga jumlah klaster yang optimal adalah 4.

Selamat! Anda sudah paham bagaimana K-Means bekerja. Sekarang kita akan belajar menggunakan K-Means dengan library SKLearn
